摘要：為了解決擺線針輪行星減速器的傳動效率低，結構不夠緊湊的問題，通過推導其傳動效率的公式，并對設計變量和約束條件進行研究，建立了以體積最小、效率最高為目標函數的優化設計數學模型。采用遺傳算法，運用ＭＡＴＬＡＢ軟件編制遺傳優化程序，調用遺傳工具箱進行優化。優化設計結果與傳統的設計相比，體積減小16.6，效率增加2.06％，優化效果顯著，從而為擺線針輪行星減速器優化設計提供一定的理論和方法。

          減速器是機械傳動中的核心部件，漸開線減速器具有廣泛的應用，但有些場合卻不能滿足使用要求。擺線針輪行星減速器具有體積小、質量輕、傳動比范圍大、壽命長、精度保持穩定、傳動平穩等一系列的優點而得到了廣泛的應用。但擺線針輪行星減速器的傳動效率卻比漸開線行星減速器的傳動效率低，因此研究擺線針輪行星減速器的參數設計，優化體積和傳動效率具有重要意義。
            由于擺線針輪行星減速器涉及的參數比較多，關系比較復雜，影響的因素也較多，這就給擺線針輪行星減速器的優化設計帶來了一定的困難。從現在所發表的擺線針輪行星減速器的優化設計論文［１］［２］１４２［３］來看尚存一定的不足，比如目標函數單一，不能有效提高擺線針輪行星減速器的傳動效率；各約束條件單位不統一，給優化設計的實現造成了一定的難度。因此全面和深入地研究擺線針輪行星減速器的優化設計問題，對擺線針輪行星減速器技術發展有一定的實用意義。本文中我們推導出擺線針行星減速器傳動效率的公式，以體積最小和效率最高作為目標函數，利用遺傳算法對擺線針輪行星減速器進行多目標優化設計。
              
１　擺線針輪減速器優化設計數學模型
  １．１　設計變量
擺線針輪傳動結構如圖１所示。現研究一級擺線針輪行星減速器優化問題，取擺線針輪行星減速器的針輪分布圓直徑ＤＺ；針齒銷直徑ｄｚ′；擺線輪寬度Ｂ；短幅系數Ｋ１；擺線輪內孔直徑Ｄ１；柱銷直徑ｄｓ′作為設計變量，即  
                      
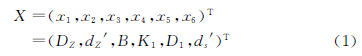
１．２　目標函數
（１）本文以在功率和傳動比一定條件下，并選定輸出機構銷軸數Ｚｓ，選擇減速器體積最小為目標函  數［２］１４２，即
                        ｍｉｎｆ１（ｘ）＝π４（ＤＺ＋ｄＺ′＋２Δ１）２（２Ｂ＋δ） （２）
         式中，Δ１為針齒套壁厚，一般取Δ１＝２～１０ｍｍ；δ為擺線輪之間的間隔，δ＝ｂ－Ｂ，ｂ為轉臂軸承寬度。 
                      
       （２）以擺線針輪行星減速器的傳動效率為另一個目標函數。
        當針輪固定時，轉臂輸入時（針輪輸出時，轉臂輸入時類似），擺線針輪行星減速器的傳動效率η 可近似用下式計算［４］３３０。
                              η＝ηｘｃηＢηＷηＢ′２ （３）
         式中，ηｘｃ為當針輪固定，減速部分的嚙合效率，ηｘｃ＝１－０．０４πＺｃＫ１（１－ｄＺ′ＤＺ）１＋０．０４πＫ１（１－ｄＺ′ＤＺ）；ηＢ為轉臂軸承的效率，其概略值為，ηＢ＝０．９９～０．９９５；ηＷ為輸出機構的效率，ηＷ ＝１－ ０．０８ＤＺＫ１ｄｓ′π［（ＤＺ－ｄｚ′－２Δ１－Ｋ１ＤＺ／Ｚｂ）＋Ｄ１］（ｄ′ｓ＋２Δ２）；ηＢ′為輸入或輸出軸上的滾動軸承的嚙合效率，其概略值為ηＢ′＝０．９９～０．９９９。
        由文獻［４］３２４－３３０經整理后，其效率計算式為
           
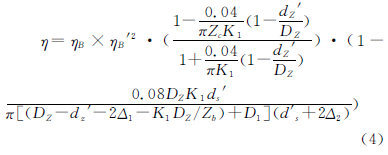
         考慮到η∈（０～１），將效率最大值轉換成最小值，則效率最大的目標函數是
                    
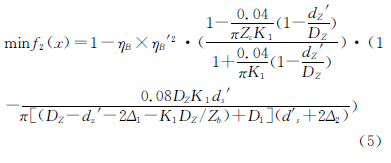
              式中，Δ２為柱銷套壁厚，一般取Δ２＝２．５～５ｍｍ；Ｚｂ為針輪齒數，Ｚｂ＝ｉ＋１；Ｚｃ為擺線輪齒數Ｚｃ＝ｉ。
１．３　約束條件的建立
（１）擺線輪齒廓不根切條件的約束條件  
            
        式中，Ｄｓ為柱銷孔中心分布圓直徑，Ｄｓ＝ｄｆｃ＋Ｄ１２；ｄｆｃ為擺線輪齒根圓直徑，ｄｆｃ＝ＤＺ－（ｄｚ′＋２Δ１）－２　Ｋ１ＲＺ／Ｚｂ，所以Ｄｓ＝［ＤＺ－（ｄｚ′＋２Δ１）－Ｋ１ＤＺ／Ｚｂ＋Ｄ１］／２；ｄｓｋ為銷軸孔直徑，ｄｓｋ＝ｄｓ＋２Ａ，ｄｓ為銷軸套外徑，ｄｓ＝ｄｓ′＋２Δ２，Ａ 為偏心距Ａ ＝Ｋ１ＤＺ／２Ｚｂ，所以ｄｓｋ＝ｄｓ′＋２Δ２＋Ｋ１ＤＺ／Ｚｂ；Δ′為銷軸孔與擺線輪內孔之間所留的一定厚度，Δ′＝０．０３ＤＺ。
            所以推得
                    
  （４）擺線輪與針齒的接觸強度條件
            由文獻［５］７４－８２推導整理得
                    
         式中，ＭＶ為輸出軸的阻力矩，ＭＶ ＝９７　３６０ＺｃＮＨｎＨ，ＮＨ為輸入功率（ｋＷ）；ｎＨ為主軸轉速（ｒ／ｍｉｎ）；Ｙ２ｍａｘ為最大接觸應力處的位置系數（由文［５］７７表１０查取）；［σｊ］為許用接觸應力（ＭＰａ）。得
                 
（５）針齒銷的彎曲強度條件
        對于雙支點針齒銷的彎曲應力，由文獻［５］８２－８５推導整理得
        
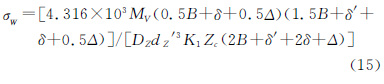
                 故約束條件為
                     
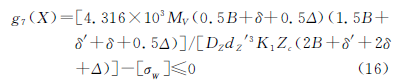
          式中，［σＷ ］為針齒銷許用彎曲應力（ＭＰａ）；δ′為擺線輪于針齒殼側面見的間隙（ｍｍ），一般取δ′＝４ｍｍ；δ為擺線輪間隔環的厚度（ｍｍ），δ＝ｂ－Ｂ，ｂ為軸承的寬度；Δ為針齒殼側面的壁厚（ｍｍ），一般為Ｂ≥Δ≥ｄＺ′。
（６）柱銷的彎曲強度限制條件為
      Ｗ 機構中的柱銷所受的最大彎曲應力由文獻［５］８５－８７推導得
            
      （８）短幅系數Ｋ 應在０．４５～０．８范圍選取，即
                   ｇ１０（Ｘ）＝０．４５－Ｋ≤０ （２１）
                   ｇ１１（Ｘ）＝Ｋ－０．８≤０ （２２）
   （９）擺線輪壁厚的約束條件［４］３１８
        擺線輪的厚度一般為Ｂ＝（０．０５～０．１）ＤＺ，故
                  ｇ１２（Ｘ）＝０．０５ＤＺ－Ｂ≤０ （２３）
                  ｇ１３（Ｘ）＝Ｂ－０．１ＤＺ≤０ （２４）
         綜上所述，擺線針輪減速器的多目標優化設計數學模型可表示為
                    
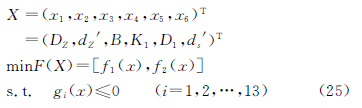
２　遺傳優化
         由于遺傳優化具有魯棒性好、全局尋優的特點［６］，為了避免陷入局部最優解，本文采用遺傳算法對擺線針輪行星減速器進行多目標優化設計。
  ２．１　求解多目標優化問題的遺傳算法
           遺傳優化中為了綜合考慮各分目標函數在相對重要程度方面的差異和量綱上的差異，使各個分目標函數能均勻一致地趨向于各自的最優解，采用加權法［７］２６。其目標函數表示為
               Ｆ（ｘ）＝ｗ１ｆ１（ｘ）＋ｗ２ｆ２（ｘ） （２６）
           綜上所述，擺線針輪行星傳動是多目標函數的優化問題。由于體積和效率兩目標函數的量綱不同，值的大小相差很大，構造統一目標函數時難以充分反映各子目標函數的重要程度，因此先將體積和效率的目標函數作無量綱處理［８］。由于在擺線針輪行星減速器中體積和效率具有同等的地位，所以我們將各單目標優化值的倒數取作權重系數。
                  ωｉ＝１／ｆｉ＊（ｘ）ｆｉ＊（ｘ）＝ｍｉｎｆｉ（ｘ） （２７）
             式中，ωｉ是作了無量綱處理后的第ｉ個子目標函數的 權重。      
       經過這樣的處理后，使各子目標函數的量綱得到了統一，在同一量綱的基礎上再對各子目標函數賦予相應的權數，最后就將多目標優化轉化為了單目標優化。按照此方法，評價函數不僅不會受到各分目標函數值相對大小的影響，還能充分反映出各單目標函數值偏離各自最優值的程度。
  ２．２　遺傳優化算法的實現
         本文采用ＭＡＴＬＡＢ 語言編制遺傳算法程序［７］２６［９］，利用ＭＡＴＬＡＢ７．０中的遺傳算法工具箱中遺傳優化函數ｇａ對擺線針輪行星減速器進行遺傳優化。先求得ｆ１（ｘ）、ｆ２（ｘ）分別為單目標函數時的最小值，然后再求多目標的最小值Ｆ（ｘ）。   
          
    ３　優化實例及結果分析
３．１　實例
        以某公司生產的Ｂ１２型減速機為設計實例，減速機的輸入額定功率Ｐ１＝１１ｋＷ，輸入轉數ｎ１＝１４４０ｒ／ｍｉｎ，傳動比ｉ＝２９，輸出機構環形槽數Ｚｓ＝１０，擺線輪和針齒的材料均采用ＧＣｒ１５軸承鋼，ＨＲＣ５８～６２，許用接觸應力［σｊ］＝１　１００Ｍａ，許用彎曲應力［σＷ ］＝２００ＭＰａ。
  ３．２　優化求解
         采用ＭＡＴＬＡＢ 遺傳工具箱進行遺傳優化，具體步驟如下：
①編寫以體積最小為單目標函數的Ｍ文件，通過調用遺傳優化函數ｇａ，求得最小體積為２　０４４　１８１；②編寫以效率最高為單目標函數的Ｍ文件，通過調用遺傳優化函數ｇａ，求得最高效率為９５．３６％；③編寫以體積最小和效率最高為多目標函數的Ｍ 文件，如圖２所示，其中體積的權重為１／２　０４４　１８１，效率的權重為１／   （１－０．９５３　６）；④調用遺傳算法主函數ｇａ．ｍ。
                 
                              
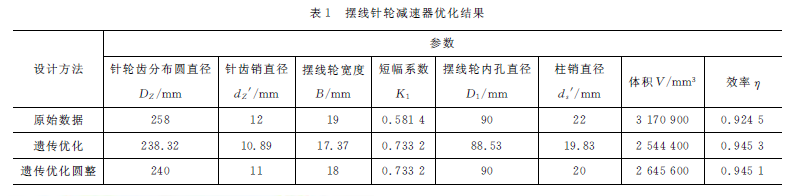
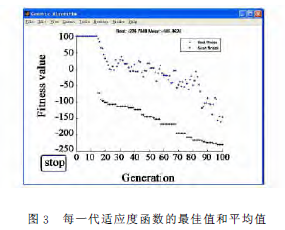
           計算結果表明：采用遺傳算法優化設計要優于常規設計方法。在保證主要傳動元件設計要求的同時，體積減小１６．６％，效率增加２．０６％ 。所以，利用遺傳算對擺線針輪行星減速器進行優化設計效果是顯著的。
          
４　結論
        分析影響擺線針輪行星減速器的主要參數，建立以體積最小和效率最高為優化設計的目標函數，并系統研究了優化的約束函數。用ＭＡＴＬＡＢ語言編制了遺傳算法程序，運用ＭＡＴＬＡＢ遺傳工具箱對其進行遺傳優化設計，在滿足強度條件的前提下，獲得比傳統方法更好的結果，使其結構更緊湊，傳動效率更高。可為擺線針輪行星減速器設計提供理論支撐。